Linear classifier function
- "Linear classifier function"은 데이터를 분류하는 데 사용되는 선형 함수를 의미합니다. 선형 함수는 데이터를 분리하기 위해 직선 또는 초평면을 사용합니다. 이러한 함수는 분류 작업에서 오류를 최소화하기 위해 데이터를 잘 분리하는 경계를 찾는 데 사용됩니다.
- 선형 함수는 일반적으로 다음과 같은 형태를 가집니다:

- "denotes +1"은 해당 데이터 포인트가 양성 클래스에 속한다는 것을 의미하고, "denotes -1"은 해당 데이터 포인트가 음성 클래스에 속한다는 것을 의미합니다.

- Maximum Margin Classifier : 데이터를 분류할 때, 클래스 사이에 가장 큰 간격(마진)을 가진 선을 찾습니다. 이를 통해 safe zone을 만들어서 새로운 데이터를 분류할 때 틀릴 가능성을 줄입니다.
- margin은 결정 경계(데이터를 나누는 선)와 그에 가까운 데이터 포인트 사이의 거리입니다. Maximum Margin Classifier 는 이 거리를 최대화하기 위해 노력합니다. 그렇게 하면 새로운 데이터가 들어와도 틀리지 않을 확률이 높아집니다. → outliners에 대한 강인함과 strong generalization ability
- strong generalization ability ; 강력한 일반화 능력(strong generalization ability)"은 모델이 학습한 데이터 이외의 새로운 데이터에 대해서도 잘 작동하는 능력을 의미합니다.
Support Vectors란?

- 결정 평면이란 데이터를 나누는 선, 평면 또는 초평면을 말합니다. 이것이 어떤 모델의 결정 경계를 의미하는데요, 예를 들어 데이터를 빨간 공과 파란 공으로 나누는 선을 상상해보면, 그 선이 결정 평면입니다.
- 그런데 이 결정 평면에 가장 가까운 데이터 포인트들이 있는데, 이것들을 'support vector'라고 부릅니다. support vector는 결정 평면과 가장 가깝습니다.. 이 support vector들이 모델이 학습하는 동안 매우 중요한 역할을 합니다. 이들이 결정 평면의 위치를 결정하고 모델이 일반적인 데이터에도 잘 작동하도록 도와줍니다.
- 모델이 학습하는 동안 모든 데이터 포인트가 아닌 지원 벡터들만이 실제로 decision surface을 만드는 데 중요하다는 것을 의미합니다.
- 결정경계 식 :

- We want: Positive Samples w𝑇x+ + b > 0
- Negative Samples w𝑇x− + b < 0


Support Vector Machine 목표는?
- 이것의 목표는 : the maximum margin (마진은 최대화)
- = 가중치 벡터의 크기를 최소화
- → 결정 경계를 찾는 과정에서는 margin을 최대화하고, 동시에 모델이 복잡해지지 않도록 가중치 벡터의 크기를 최소화하는 것이 중요합니다


(margin 구하는 방식 : 유클리드 방식임)
- 서포트 벡터들에 대한 제약 조건(constraint)

- 커널(kernel)"은 SVM(Support Vector Machine)에서 비선형 문제를 해결하기 위한 강력한 도구입니다.
- SVM은 기본적으로 선형 분리가능한 문제를 다루는 모델입니다. 그러나 많은 실제 세계의 데이터는 선형적으로 분리할 수 없는 비선형 문제일 수 있습니다. 이런 경우에 SVM을 사용하려면 데이터를 고차원으로 매핑하여 선형 분리가능한 문제로 바꿔주어야 합니다.
- → 이때 사용되는 것이 커널 함수입니다. 커널 함수는 고차원 공간으로 데이터를 매핑하는 함수로, 비선형 문제를 해결하기 위해 사용됩니다. 커널 함수를 사용하면 고차원 공간에서의 선형 분리가능한 문제를 효율적으로 해결할 수 있습니다
- Ex) RBF kernel:

→2차원에서 3차원으로,,,
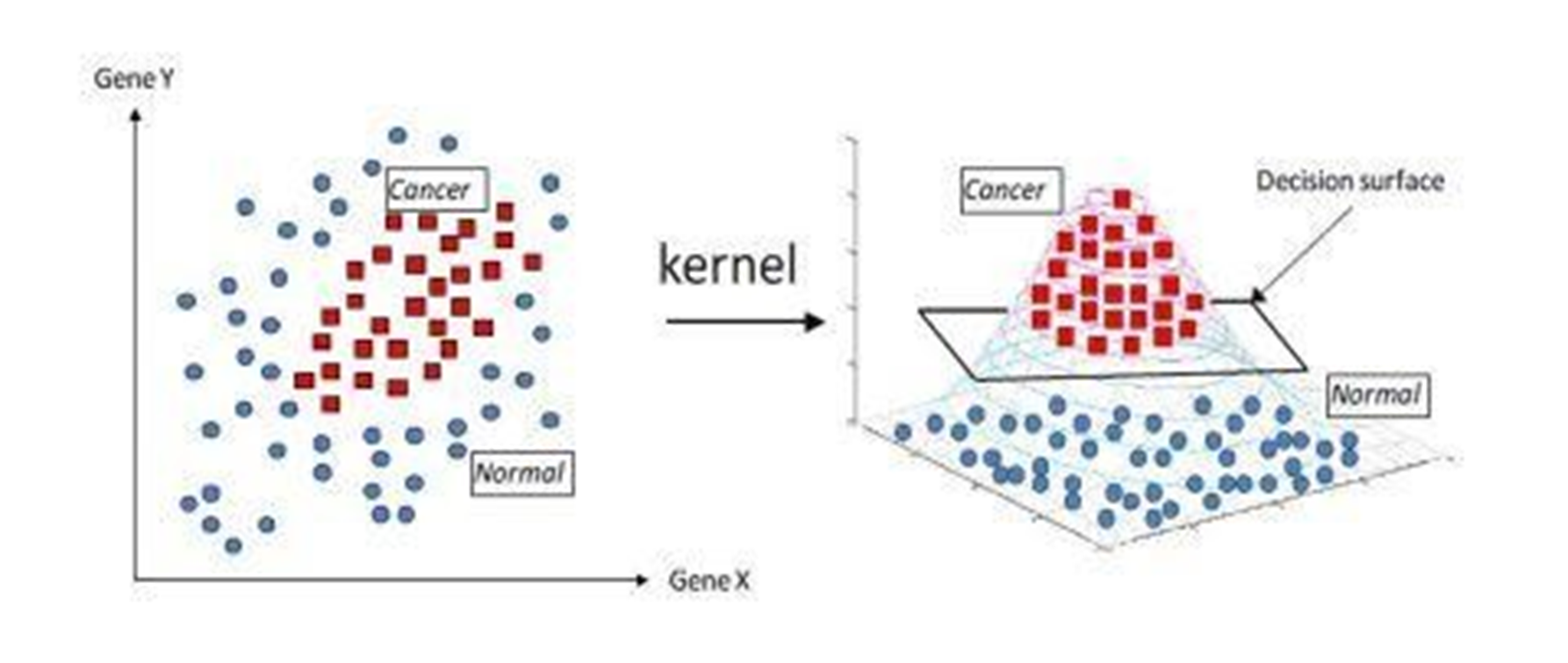
커널 기법은 데이터를 더 높은 차원으로 매핑하여 선형으로 분리 가능한 문제로 변환하는 방법을 사용합니다. 이를 "커널 트릭(kernel trick)"이라고도 합니다.
원래 선형으로 분리되지 않는 데이터를 고차원 공간으로 매핑하면, 고차원 공간에서 데이터가 선형으로 분리되는 경우가 많습니다. 이를테면, 2차원 데이터가 직선으로 분리되지 않지만, 3차원 공간으로 매핑하면 평면으로 분리될 수 있습니다.
Support Vector Machine (SVM)은?
- 지도 학습 알고리즘으로, 모든 데이터에 대한 정답(라벨)이 이미 존재하는 상황에서 사용됩니다. 이 알고리즘은 데이터를 분류하기 위해 선형 함수(분류기)를 찾습니다. 이때, 선형 함수를 찾는 과정에서는 서포트 벡터라 불리는 특정한 데이터 포인트들을 기준으로 하며, 이들 간의 간격(마진)을 최대화하는 선을 찾습니다.
- 서포트 벡터란, 결정 경계와 가장 가까이 있는 데이터 포인트를 말합니다. 결정 경계와 서포트 벡터 간의 거리가 최대가 되도록 결정 경계를 설정함으로써, 새로운 데이터를 분류할 때 더욱 견고하고 일반화된 분류를 할 수 있습니다.
SVM 장점 및 효율
- Efficient: Use support vectors only (ignore other samples)
- SVM은 분류를 위해 서포트 벡터만 사용하며, 다른 샘플들은 무시합니다. 이는 연산량을 줄여주어 고차원 데이터에 특히 효율적입니다.
- Reduced computation – good for high dimensional data
- SVM은 연산량을 줄여주는 특성이 있어, 고차원 데이터에서 효과적으로 작동합니다. 이는 데이터의 차원이 많을수록 계산이 복잡해지는 상황에서 유용합니다.
- Powerful: good classification performance when combined with sophisticated hand-crafted features (pre-processing) and kernel methods (nonlinear classification)
- SVM은 고급 기법과 커널 메소드를 결합하여 사용하면 우수한 분류 성능을 보입니다. 이는 사전 처리(pre-processing) 기법과 다양한 커널 함수를 활용하여 비선형 분류에 사용할 수 있음을 의미합니다.
- Used in almost all the state-of-the-art (SOTA) classification tasks before Deep Learning becomes popular (until ~2011)
- SVM은 딥러닝이 인기를 얻기 전까지 대부분의 최신 분류 작업에서 사용되었습니다. 특히 2011년까지 SVM은 많은 분야에서 최고의 성능을 보였습니다.
- types of norms : defines the size of vector




Visualization of L2-norm
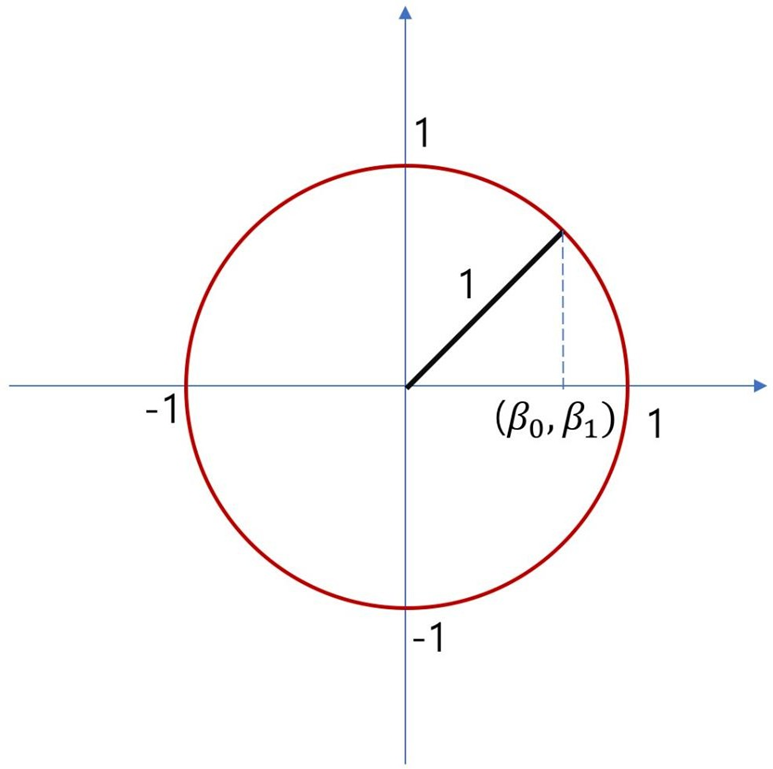
Visualization of L1-norm
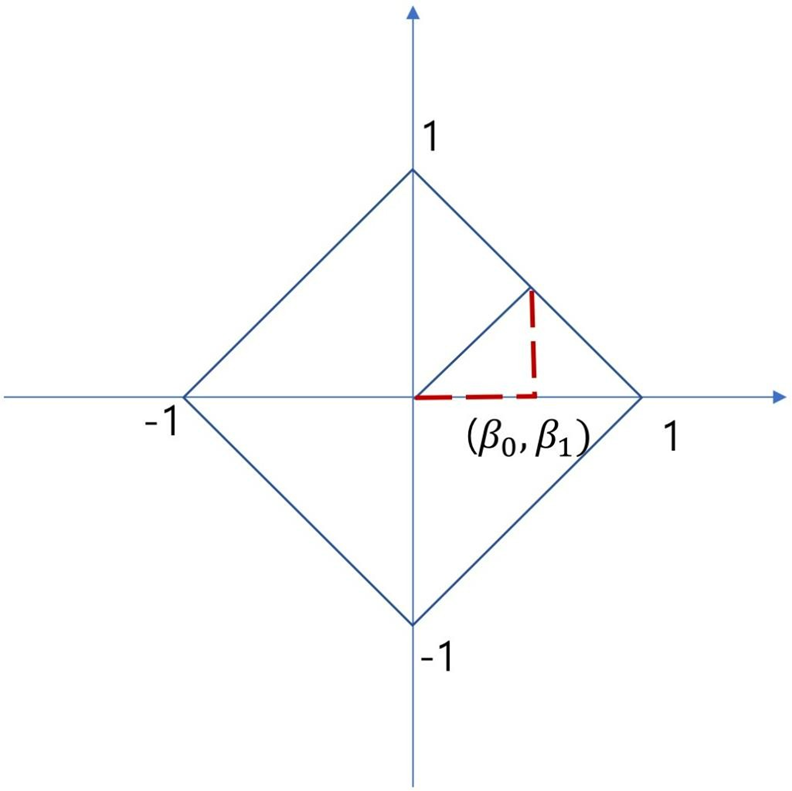
- Loss: distance induced by ℓ𝒑-norm
Target label (=y): 모델이 예측하고자 하는 실제 값입니다. 보통 이것이 정답으로 사용됩니다.
Output vector(=f(x)): 모델이 주어진 입력에 대해 예측한 값입니다. 이것은 모델의 출력이며, 함수 f(x)로 표현됩니다.
Error(y-f(x)) : 목표 레이블과 출력 벡터 사이의 차이를 의미합니다. 일반적으로는 목표 레이블에서 출력 벡터를 뺀 값으로 계산됩니다.
Loss: (size of error) 손실은 오차의 크기를 나타냅니다. Lp-Norm을 사용하여 오차의 크기를 측정하며, 이는 오차를 어떤 기준으로 측정하는지를 나타냅니다. 여기서 Lp-Norm은 벡터의 크기를 측정하는데 사용되며 p 값에 따라 측정 방법이 달라집니다.
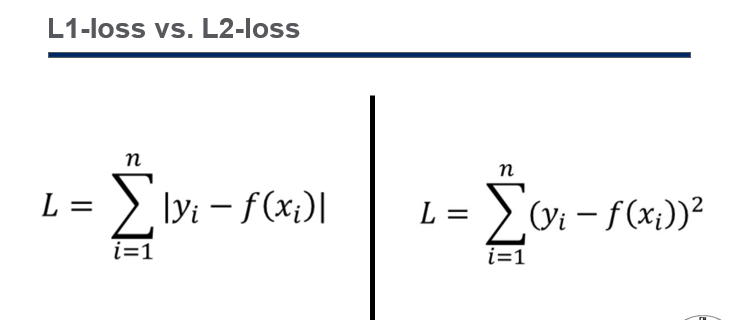
'기계학습심화' 카테고리의 다른 글
| 기계학습심화 2단원 정리 (2) (1) | 2024.10.23 |
|---|---|
| 기계학습심화 2단원 정리 (1) (0) | 2024.06.24 |
| 기계학습심화 1단원 정리 (2) | 2024.05.28 |


